引言

随着大数据时代的到来，数据量的激增使得实时数据处理变得尤为重要。在许多应用场景中，如金融交易、网络监控、实时分析等，都需要对数据的变化率进行实时计算。数据实时变化率计算程序能够帮助我们快速了解数据的动态变化，从而做出更准确的决策。本文将介绍数据实时变化率计算程序的设计与实现，旨在为相关领域的研究者提供参考。

数据实时变化率的概念

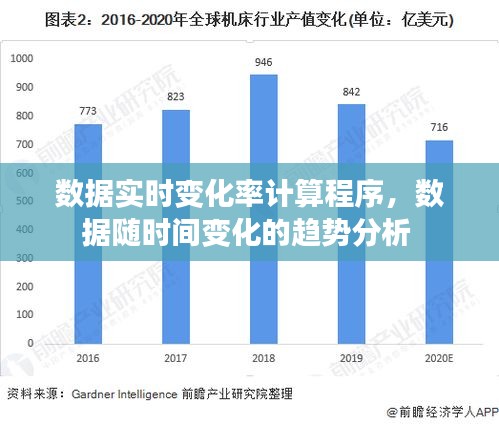
数据实时变化率是指在一定时间窗口内，数据值的增减幅度与时间窗口的比值。它能够反映数据在短时间内变化的快慢程度。计算数据实时变化率对于实时监控、预警和决策支持具有重要意义。

数据实时变化率计算方法

数据实时变化率计算方法主要有以下几种：

• 差分法

• 滑动窗口法

• 指数平滑法

• 卡尔曼滤波法

以下将详细介绍这几种方法。

差分法

差分法是最简单的一种计算数据实时变化率的方法。它通过计算相邻两个数据点之间的差值来得到变化率。具体公式如下：

变化率 = (当前数据点 - 前一个数据点) / 时间间隔

差分法简单易实现，但容易受到数据噪声的影响，对于数据波动较大的场景，计算结果可能不够准确。

滑动窗口法

滑动窗口法是一种常用的数据实时变化率计算方法。它通过在数据序列上滑动一个固定大小的窗口，计算窗口内数据的变化率。具体步骤如下：

1. 确定窗口大小。

2. 计算窗口内数据的变化率。

3. 将窗口向右滑动一个数据点，重复步骤2。

滑动窗口法能够有效降低数据噪声的影响，提高计算结果的准确性。但窗口大小的选择对计算结果有较大影响，需要根据实际情况进行调整。

指数平滑法

指数平滑法是一种基于加权平均的思想来计算数据实时变化率的方法。它通过给最近的数据点赋予更大的权重，来反映数据的变化趋势。具体公式如下：

变化率 = α * (当前数据点 - 前一个数据点) + (1 - α) * 前一个变化率

其中，α为平滑系数，取值范围为0到1。指数平滑法能够有效平滑数据波动，但需要根据实际情况调整平滑系数。

卡尔曼滤波法

卡尔曼滤波法是一种基于状态估计的实时变化率计算方法。它通过预测和修正来估计数据的变化趋势。具体步骤如下：

1. 建立状态模型。

2. 初始化状态估计值和误差协方差。

3. 根据观测数据更新状态估计值和误差协方差。

卡尔曼滤波法适用于复杂的数据变化场景，能够有效处理数据噪声和突变，但实现较为复杂。

数据实时变化率计算程序的设计与实现

基于以上几种计算方法，我们可以设计一个数据实时变化率计算程序。以下是一个简单的Python示例：

import numpy as np

def calculate_rate(data, method='difference'):
    if method == 'difference':
        return np.diff(data) / np.diff(np.arange(len(data)))
    elif method == 'moving_average':
        window_size = 5
        moving_avg = np.convolve(data, np.ones(window_size) / window_size, mode='valid')
        return np.diff(moving_avg) / np.diff(np.arange(len(moving_avg)))
    elif method == 'exponential_smoothing':
        alpha = 0.2
        smoothed_data = np.zeros(len(data))
        smoothed_data[0] = data[0]
        for i in range(1, len(data)):
            smoothed_data[i] = alpha * (data[i] - data[i-1]) + (1 - alpha) * smoothed_data[i-1]
        return smoothed_data
    elif method == 'kalman_filter':
        # 初始化卡尔曼滤波器参数
        # ...
        # 更新卡尔曼滤波器
        # ...